About fun

fun is an open-specification instruction-set architecture (ISA) for structured combinator graph reduction, originally developed at the School of Electronic Information and Electrical Engineering of Shanghai Jiao Tong University. Its goal is to bring functional programming down to the architecture layer, avoiding the inconveniences and troubles of imperative programming that plague conventional ISAs.

The specification of the ISA is released under a Creative Commons Attribution 4.0 International License.

Features

fun is a purely-functional instruction set architecture that defines a language based on structured combinators, for applications where isolation, purity and the way computation is actually performed are the central concerns. fun is:

• An open, free and community-driven instruction-set architecture;
• The first purely-functional instruction set based on combinators to follow a modern, proven path of other RISC architectures;
• A purely-functional instruction set for which memory handling, control flow and other stateful and effectful behaviors is unrepresentable.
• An instruction set for efficient implementation of high-level purely-functional programming languages.

fun in one page

Basic Set

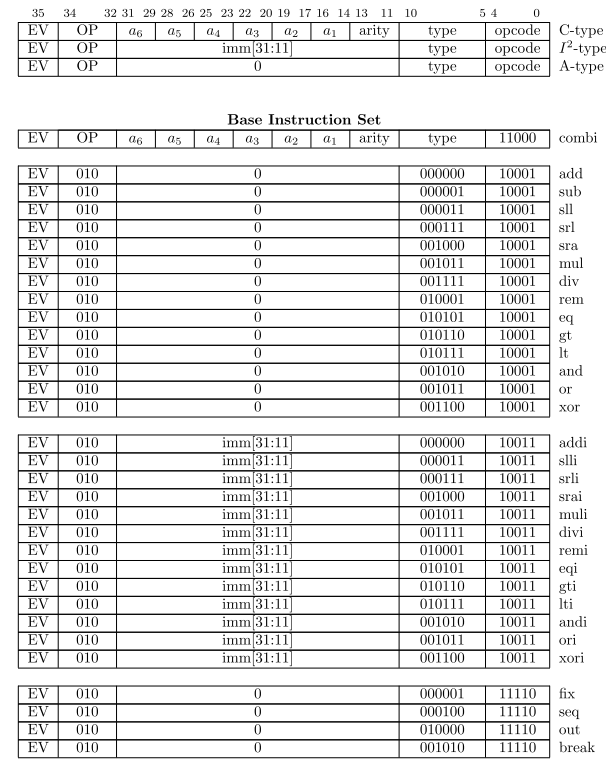
The basic set of fun instructions is composed by instructions of three types: C, I2 and A.

Combinators

Instructions of type C can represent structured combinators with up to 6 nodes, in 64 reduction [patterns](/files/patterns.pdf) (type). These combinators can consume up to 8 nodes on reduction (arity).

Arithmetic and Logic

Type I2 is allocated for instructions that depend on immediate values, such as arithmetic and logic instructions. General instructions are represented via type A.

Graph Reduction

The basic set includes instructions for managing graph reduction such as fixed-point (`fix`, or Y combinator), force strict-evaluation (`seq`), data output to the peripheral bus `out`, and debugger breakpoint `break`.

Why Combinators?

Combinators are a symbolic representation for functions that dates back to the work of Moses Schonfinkelin the late 1910s and early 1920s. They form a language that is able to represent *any* computable function, but do not require an specific machine model. Our reasons to continue research with combinators are as follows:

• • Machine-independent, instruction-set-level language
  • Formal model that does not require complex operational rules. Pure, untyped lambda-calculus is included in a combinatorial ISA by default.
  • Computation without control-flow.

In a practical setting, combinators do not require instructions for arbitrary memory handling (load, store, move), branches and jumps. Moreover, combinators help us isolate pure computation from impure IO. The result is a machine language that is algebraically transformable, where intentional effects are isolated from programs without loss of expressivity. In other words, combinators bring safety and security as a default, not as an afterthought.